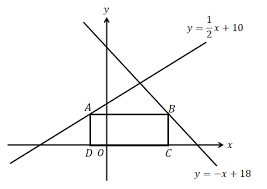期末テスト前 中学2年生で明確に分かる学習適性と努力適性
多くの中学の学習進度に合わせて書いています。当てはまらない進度の中学もあります。
努力する力が明確に分かる国語
この時期、平家物語や徒然草と言った古文、それに漢詩を学習する学校が多いと思います。この範囲は成績の良い生徒取っては簡単に得点できる範囲であり、成績の良くない生徒にとっては全く得点できない範囲なのです。
理由は簡単で、中学の古文では高校のようにややこしい文法を学ぶわけではありません。せいぜい係り結びと「き」とか「たり」の過去・完了の助動詞くらいです。それに加えて、せいぜい10~20の古語だけです。歴史的仮名遣いと言ったところで大したものではありません。これくらいをおぼえて、教科書に対訳してある、あるいは先生が現代語訳した内容を「そうなんだ~」と見ていれば十分なわけです。
漢詩にしたって、置き字や再読文字や否定語などの面倒な文法は学習しません。簡単なレ点と一二点くらいです。とても簡単に学習できます。多少の暗記で大丈夫なわけです。
この丸暗記学習は成績上位、公立中学で言えば通知簿4の上半分、テストで80点くらいは確実に取ってくる生徒に関しては楽勝の分野です。現代文の長文読解で「なんでその答えになるねん!」という問題がないだけ学習が楽なはずです。
一方、通知簿が4の下半分、70点代行ったり行かなかったりする生徒は、この簡単な暗記ができません。古文や漢詩のとっつきにくさで嫌になって、嫌いな努力が余計に億劫になるからです。
この差は明確で、学習適性と努力適性を見るのに最適な学習分野です。ここで「出来ない」など言う子供は「学習ができない」のではなく「努力ができない」と言っているに等しい。この段階で学歴で飯を食うことは難しいと思います。
基礎学習が出来ているか分かる理科
理科では化学式と電気を学ぶ学校が多いです。
化学式では化学記号の暗記、それに中学2年生では「反応する手の数」というような表現で学ぶ結合数をおぼえて、実際の化学反応式を見て「ほう~、そうか」で終わりです。楽勝と言っていいでしょう。
ところが、国語の欄に書いた下半分では、まずこの馴染みのない化学記号を暗記できない。暗記しても、この反応の手の数が化学反応式と結びつけて考えられない。簡単なことなので、反応の手の数と化学反応を説明するとその時は理解できるのですが、「だから、こうなっている」と自分で出来るようになるまで考えず、「分かった!」で放置して忘れるからです。
電流では、もう公立中学では半数以上は無理です。だって、小学校5年生でつまずいて時速や%の単位計算が怪しい生徒が相当数いるのです。オームの法則なんかできるわけがありません。
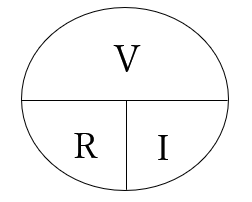
ましてやE=RIという公式を、じゃあIが一定な直流では抵抗と電圧は比例関係とか、Eが一定な並列は抵抗と電流は反比例なんか到底理解できません。だから、関係式で教えずに図で教える学校や塾も多い。もうこの段階で理数系終了です。下に紹介する関数なども不可でしょう。
今後の学習に適応できるか分かる数学
数学では一次関数を学習する学校が多いはずです。
一次関数では応用問題で抽象的思考と論理的思考が必要になります。
例えばこの問題です。この問題では座標Aをaやtといった変数でAの座標を考えなければいけません。まずこの「例えばこうなって・・」という抽象的な志向が半分以上の子供が受け付けません。
もしそう考えられても、次は「じゃあ長方形ならAのY座標とBのY座標が同じだから、関数の式からBのX座標が求められるよね・・。」これで2/3の生徒はアウトです。だから「ADはAのY座標だから、ABというX座標間の差と同じ。」という論理的展開が分からない。
だから、関数の応用問題は多くの生徒が苦手としています。これは訓練だけでは手に入れられる能力ではないので、これ以後数学は「丸暗記」に塾は走り出します。学年が上がるごとに丸暗記は複雑化し、多数化し、高校で破綻します。
この関数の問題ができない生徒は、中学2年生の段階で受験に数学がない私立文系は確定です。