中学２年生で一発で分かる「関関同立は絶対無理」な生徒／勝ち目は付属高校一択！

この問題が解けない生徒は関関同立は無理です

探しても問題がないから自分で作ります。

公立中学なら通知簿５しか解けないと思います。

もし違うとお考えなら、お子さんで試してください。

なぜできないのか？

私が自分で問題を作ったように、この問題は、非常にレアな問題です。なぜレアか？　ほとんどの子供ができないばかりか、教えても理解できないからです。y=ax+3のaである変化の割合の意味を公立中学なら半分の子供は分かっていないし、その「変化の割合」という抽象的な概念を具体化して考えられないのが4/5の中学2年生だと思います。だから絶対評価で上位20％の通知簿5しか解けません。

それに、解法が2段階以上になっているから「テスト１日前にこの問題やった～」の解法丸暗記ではおぼえきれない。大多数の中学生ができない理由は、「この式にこの座標を代入する。」程度の1段階の解法丸暗記しかできないからです。「こういうことを聞いている問題だった。だから、こう解いたんだった。」と理屈で考えられるのは、限られた生徒だけです。

この問題では、まずaの変化の割合の抽象的な概念が分かっていないと解けません。そして、次に座標を2段階で代入できないと解けない。aが正の場合(-1,-2)という座標を通ることが分かっているんだから、y=ax+3のaが出せる。そこで関数の式が決まれば (3,b)の座標を代入してbが出るとは、2/3以上の中学2年生は考えられない。この問題は、教えてもA→BそれでB→Cと理屈が2段階あるので、頭がついていかない。条件をすべてごちゃ混ぜで考えるから、思考順序の整理ができない。だから解法を自分では再現できないんです。

そして、aが負の場合では地学結果が出る。負の場合は(3,-2)という座標が分かっているんだから、同様にaを出して(-1,b)を求めなければいけない。この場合分けなど、ほとんどの子供に出来ない。y=ax+3という抽象的な文字の羅列を具体的な思考回路に落とし込めないからです。

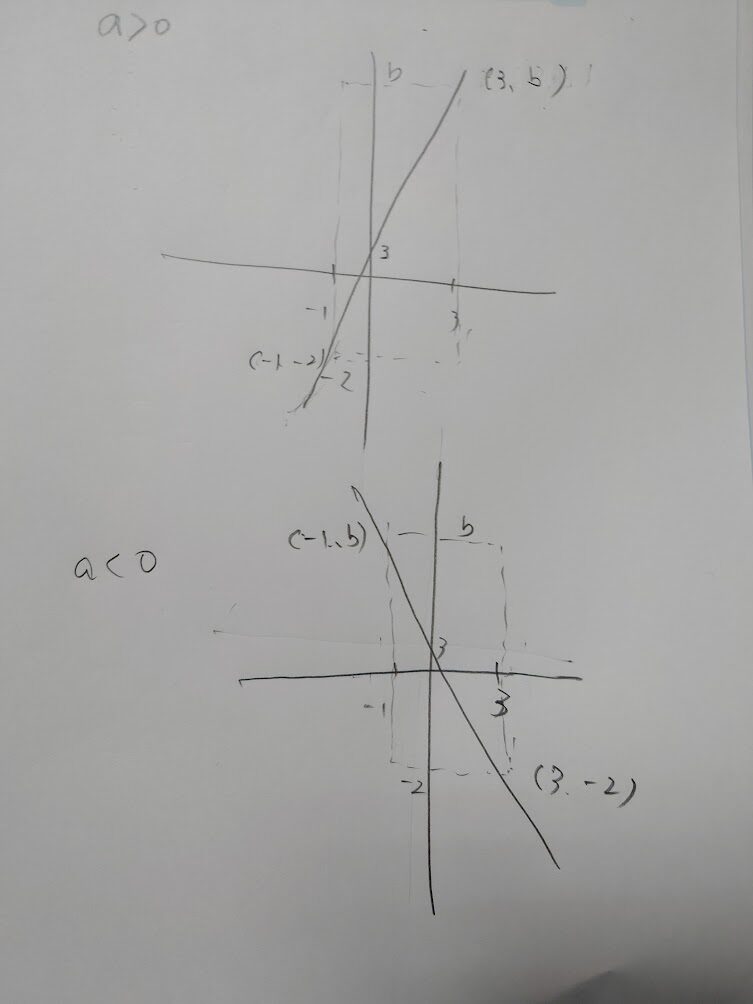
でも、理解力がある子供なら、この図を書いて説明すると一発で「ああ、そういうことね」と納得します。教えるのに2～3分しか必要ありません。この格差は、もう埋めようがなく、どう教えても無理です。教え方の問題ではなく資質の問題だからです。

この2問を教えて理解できない中学2年生は大学受験で関関同立は無理です

だって、論理的展開も抽象的な思考も出来ないわけです。「A＝B,B＝CはOK、でもA＝Cは分からない。」わけです。1年半後に始まる高校の学習には、おそらく全くついていけません。

悲劇は、こういう問題までも含めて中学入試や高校入試で丸暗記に邁進して、凄い努力をして、ソコソコの進学校に真ん中から下の成績で入った子供です。必死の丸暗記学習で公立中学なら４と５が混じった学力の子供たちです。

だって、自分は1教えられたら１丸暗記して半分忘れるんです。でもこの問題を理解して解ける相手は１教えたら１理解して10に応用できる。努力などでは勝負できない。それで、論理力があり適当に努力して軽々とワンランク下の学校に入った生徒に丸ごと抜かされる。これが「大学入試で逆転する学校間格差・逆転は難しい校内格差／上位校に下位で進んではいけない理由／哀れさえ感じます」ということです。

子供本人も親も「優等生だ」「デキる」と思っているが、高校の応用力が必要で、類題など数えきれないほどあって丸暗記では全く対処できない学習を私学校では凄い速度で進まれて、にっちもさっちも行かなくなって落ちこぼれます。

だって進学校はこの「１を教えると１０に応用が利く」子供を対象に授業を進めるわけです。進学校で関関同立に苦労して合格させても宣伝にならない。だから、進学校の半分以上の生徒は授業についていけず理解不足になる。下位の高校で易しい授業を受けてしかkりと理解できている生徒にまで負けて、優等生のプライドが根っこから折られてズタボロになって大学受験に失敗するんです。