公立中学の中学3年生が今学習している二次関数と、私立中学3年生が学習する二次関数の違い
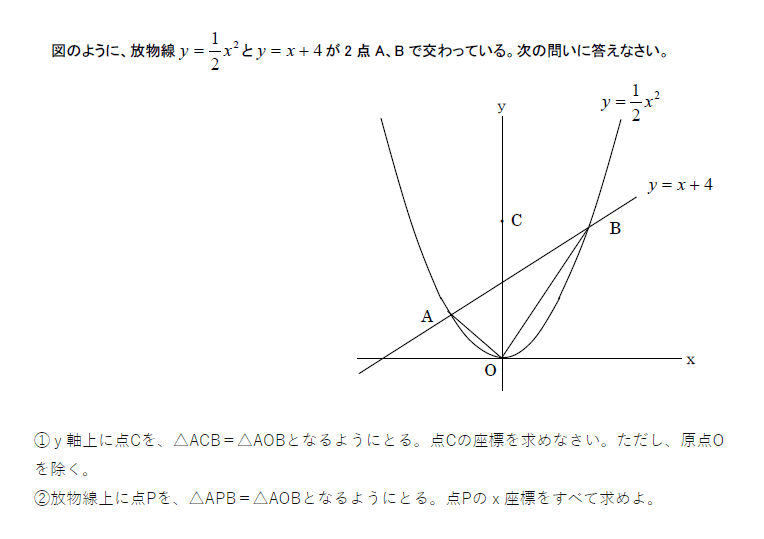
公立中学3年生が秋に学習する二次関数
公立中学で学習する応用問題で、ちょっとした進学高校の入試問題に出るのは、せいぜいこの程度です。そう難しくないもない等積変形の問題です。これが難しくてできない? この問題が出来ない生徒は、塾で何回教えても出来ません。関数の座標代入と等積変形という2段階の理屈になっているので出来ないのです。あるいは、等積変形という自分で線を引かないといけない抽象的な概念が理解できないのです。教え方の問題ではなくにキャパオーバーです。
論理的な思考ができる、抽象的な思考を可視化できてこの問題がテストで解ける生徒は通知簿が4の上位以上だと思います。でも、この中には理屈より解法丸暗記で解く生徒もかなりいます。単純な解法だから丸暗記で出来ますが、以下の高校の学習では無力になります。
私立中学3年生が塾で解いていた問題
上位3割が神戸大学以上、真ん中の成績では関関同立という、少し上等な私立中高一貫校の中3が先日解いていた問題です。
上の問題でつまずく子供は、おそらくいくら努力しても到底解けないと思います。上の問題がすんなり解けた生徒でも、多くの生徒は解けません。上の理屈は2段階くらいですが、これはそれが数段階になるからです。おまけに、各ステップで抽象的な思考を可視化する必要がある。この問題を解けない多くの生徒は、このかしかができずに下のようなグラフが書けません。だから、解法丸暗記で解こうとします。でも、条件が変わればグラフも移動するので丸暗記だけでは無理なのです。
中学の数学のワンステップの理屈を丸暗記で乗り越えて高得点を取って進学校に進んでいても無理です。条件によって方向性が変わる多段階の論法など丸暗記中心の学習で対応出きるはずがないからです「高校の学習でつまずく生徒とそうでない生徒の差」「中学の数学は楽勝でも高校の数学で落ちこぼれる子供」「中学の数学は優秀、でも高校の数学で落ちこぼれる生徒の特長」。
こういう考え方は関数に限らず数学の応用問題の根底をなす場合分けの解法理解が必須で、この問題が出来ないと以後すべての数学の分野はできません。この問題を中学3年生でも公立高校で1年生でも、教えられて「そうか~」と出来る生徒は、関関同立以上に進める能力はあります。あとは継続的な努力が出来るかどうかです。
一方で、この問題を何度復習してもテストで再現できない生徒は、これを解いていた進学校でも半数ぐらいはいます。だから真ん中少し上で関関同立なのです。この問題が出来ない生徒はさっさと数学を捨てて英国社の3教科で関関同立を目指すべきです。何度も学習しても出来ないことを、これから何度も学習しても出来るようにはなりません。勉強方法も努力の問題もありますが、一番大きな問題は数学的思考の適性がないということです。だから何度復習しても出来るようにならないのです。
だから、最適の数学の学習方法は数学を捨てて私立文系に絞ることです「国立大学志望に見切りをつける最後のチャンス/高校2年の秋」「

以上より
私立の進学校は、中学3年生のこの時期には公立高校の1年生の学習範囲を半ば以上終えています。「公立校の皆さん、私立中学で使っている「体系数学」と言う教科書の意味が分かっていますか?」に書いた通り、中学の学習は1・2年生で終えているからです。
この学習内容の圧倒的な差は、公立は数Ⅲを高校3年生まで引っ張り共通テストの準備もままならない状態の一方、私立は2年生で終わって3年生は受験勉強の発展学習や共通テストの準備に専念できる差を生みます。数ⅡBあたりを高校2年生で終える文系ならいざ知らず、理系で有名大学や医学科に行きたければ、そもそも公立など行くのが間違えているということがこの2枚の写真からでも分かります。
私立の中学3年生でこの問題を解ける生徒は数学を頑張って神戸大学以上を目指してください。私立の理系に落とすかは2年生の秋くらいの判断でいいと思います。それまでは勉強する科目は英数中心で差はないですから。高校1年生で解てけている公立の生徒は、理系より国立文系に進んだ方が入試ではいい結果を生む可能性が高いです。理系に進むとスケジュール的に私立優位は揺るぎません。国公立の医学部などは公立出身者はほぼいません。2つ目の図の問題が中学3年生・高校1年生で出来ていない生徒は、私立文系に専念してください。数学に時間を取って学習していても上位国立に届く学力にはなりません。数学の勉強で英語や国語にしわ寄せがいけば関関同立も行けなくなります。


