関西の有名私立大学の数学はチャート式レベル
関西学院の理系でこのレベル
昨年度の問題です。前期理系の最終問題。チャート式レベルの基本問題と言ってもいいと思います。

今回は解答をコピペします。こんな式、キーボードで書いてられまへん。
(1)と(2)の解答は教科書レベルです。これを解けないというのでは、学校を休んでいた以外にあり得ないレベルです。

じゃあ、不定積分は?
最初の二つはlogX’=1/xを使って部分積分を使えば割と簡単に解けますよね。e^xやlogx/xで部分積分を使うのは、定石です。まあ、どう考えても最初の二つは解けますね。最後の(logx)^2/x^2のヤツも同じように部分積分で考えると、1/x^2=(-1/x)’で{(logx)^2}’=2logx/1/xで両方かけるとlogx/x^2となってすぐ上の積分が利用できるのが分かります。こういう問題では、上の解を使うのも当たり前ですよね。

最後のよくある体積問題は?
おおよその図形は(1)と(2)で分かっています。唐突に(3)の計算をさせたのは、ここで使うつもりだったと推測できます。
こういう体積の問題は図形が簡単な関数で表される円の面積を積分して求めます。ということは、接線が作る下図の三角錐からf(x)が作る円錐もどきを取り除くとすると、Tの部分がでます。この三角錐もどきは、f(x)を半径として円の面積であるπf((x))^2を積分すると出ます。
ということで、(3)でわざわざf(x)^2=logx^2/x^2の不定積分を出した理由がここで分かった段階で「オッ、解けた」と合格の確信となります。
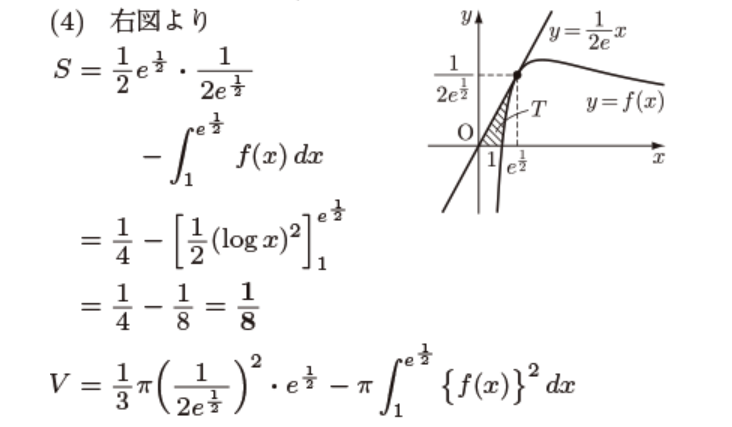
というように、関西の名門、関学でもチャート式と同レベルです
「国立大学の数学、入試問題の風格あり。 どれだけの努力が必要か分かります?」で挙げた国立大学の問題のように、題意を把握して自分で解法の端緒を見つけて解きださないといけないことはありません。チャート式に乗っているような定型の基本問題が出るだけです。だから、関西の私立の入試問題はセンター入試レベル止まりなんです。私立でも早稲田や慶応とは全く違います。
仮にも、関学を滑り止めに使うのなら、こんなもの全問解けないと本命の国立大学はカスリもしませんで。
名門大学でも、これで6割取ったら通るんです・・・。
だから、もっと易しい小問ばっかりの大問1で得点を稼いで、この問題は(1)(2)と(3)の最初の簡単な二つの不定積分くらい解ければいいということになります・・・ホンマ、教科書レベルです。なんで予備校や塾に行かないと合格できないと言う方がいるのか、私にはサッパリ分かりません。
だから、こんなことすらできない生徒は「さぼっているに等しい」「受験生としての資格はない」と言っているんです。逆に言えば、よほど学習適性がない場合を除いて、少し頑張ればなんとかなるということです。普通の生徒なら、毎日キチンと勉強さえしていれば、クラブ活動も友達との交遊も楽しみながら入学できると思いますよ。「キチンと塾に来てもらえれば、甲南大学くらいには放り込みます」に書いた通りです。
ホームページはコチラ
コメントは受け付けていません。


